The Advanced Encryption Standard, otherwise known as Rijndael (which was its original name), is one of the most widely used ciphers for the encryption of data. It’s been approved by the US government to protect classified data. In this article, I’ll explain how AES works and why it’s secure.
Galois field theory
AES makes extensive use of Galois field theory, which I’m going to give a very brief introduction to. For more details see Galois Field in Cryptography.
A Galois field is a field containing a finite number of elements. A field is a set on which the operations of addition, multiplication, subtraction and division meet certain rules. We’ll refer to these rules as they come in useful – don’t worry too much about them.
There’s the field of real numbers and the field of rational numbers. What makes a Galois field different from these fields, is that it contains a finite number of elements (which is why it’s also called a finite field). On the other hand, there is an infinite number of real numbers and rational numbers.
A Galois field is denoted as \(GF(p^n)\) where \(p\) is a prime number and \(n\) is a positive integer. We call \(p^n\) the order of the field. The elements of a Galois field are the set of elements \(\{0, 1, 2, \ldots, p^n - 1\}\).
Galois field arithmetic
Firstly, let’s take a look at \(GF(p)\). Addition and multiplication is done similarly to integers, followed by modulo \(p\) (this is just finding the remainder after dividing by \(p\)). For example, in \(GF(5)\), \(4 + 3 = 7\) is reduced to \(2\), and \(4 \times 2 = 8\) is reduced to \(3\).
Elements of \(GF(p^n)\) can be represented as polynomials of degree less than \(n\). For example, in \(GF(3^3)\), the polynomial \(x^2 + 1\) would represent 10 and the polynomial \(2x^2 + x + 1\) would represent 22, with \(x = 3\). In addition, we use modulo \(3\) on each of the coefficients. Adding up the two polynomials gives us \(3x^2 + x + 2\), which is reduced to \(x + 2\), represented as 5.
However, things get more complicated when it comes to multiplication. Take the polynomials \(2x^2 + 1\) and \(x + 1\). Multiplying these two would give us \((2x^2 + 1)(x + 1) = 2x^3 + 2x^2 + x + 1\). At this point, we’ve exceeded the order of the field! The way to resolve this is to modulo a suitable polynomial, by long division. There are certain rules for selecting this polynomial, which I will not discuss.
Use of Galois field theory in AES
In AES, where we want to manipulate bytes, \(GF(2^8)\) is used. \(GF(2^8)\) has a set of elements which represent all possible values of a byte. The fact that the addition and multiplication operations are closed (that is, applying addition and multiplication to any two elements will always return an element that is in the set of elements of that field) makes the Galois field very convenient for manipulating bytes, as operations can be done on any two bytes to get a new byte.
It also turns out that addition of two elements in \(GF(2^8)\) is simply XOR of both elements – this means that addition is efficient on hardware! On the other hand, multiplication is more complex. AES uses the polynomial \(x^8 + x^4 + x^3 + x + 1\), and most implementations will use a lookup table instead of computing the polynomial for the sake of efficiency.
Overview of AES
Now that we’re done with basic Galois field theory, it’s time to take a look at how AES is implemented.
AES can be represented by two functions, \(E(k, p)\) and \(D(k, c)\) where \(k\) is the key, \(p\) is the plaintext and \(c\) is the ciphertext. The former represents encryption, and the latter represents decryption. A valid encryption scheme would ensure that \(D(k, E(k, p)) = p\) for any \(k\) and \(p\).
AES has 3 key sizes: 128, 192 and 256 bits. It is known as a block cipher; that means it encrypts plaintext in seperate blocks of fixed size, as opposed to a stream cipher which encrypts plaintext bit by bit. Its block size is 128 bits.
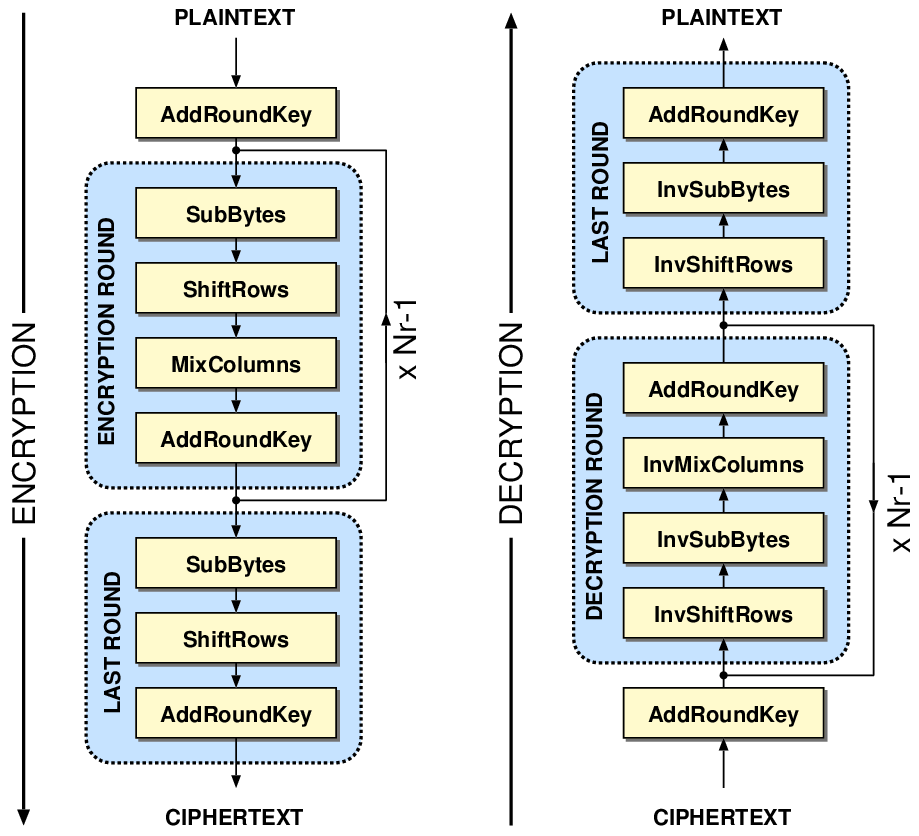
AES takes in 16 bytes, \(b_0, b_1, \dots, b_{15}\), which are arranged in a matrix from top to bottom, left to right:
\[ \begin{bmatrix} b_0 & b_4 & b_8 & b_{12} \\ b_1 & b_5 & b_9 & b_{13} \\ b_2 & b_6 & b_{10} & b_{14} \\ b_3 & b_7 & b_{11} & b_{15} \\ \end{bmatrix} \]
AES can be broken down into 4 steps:
SubBytesShiftRowsMixColumnsAddRoundKey
These 4 steps make up a round. Before the first round, AddRoundKey is
performed, and in the last round, MixColumns is omitted.
The number of rounds for AES is based on the key size:
- AES-128: 128 bit key, 10 rounds
- AES-192: 192 bit key, 12 rounds
- AES-256: 256 bit key, 14 rounds
Substitution Permutation Network
AES has a structure known as a substitution-permutation network (SPN), which takes in plaintext and keys as inputs.
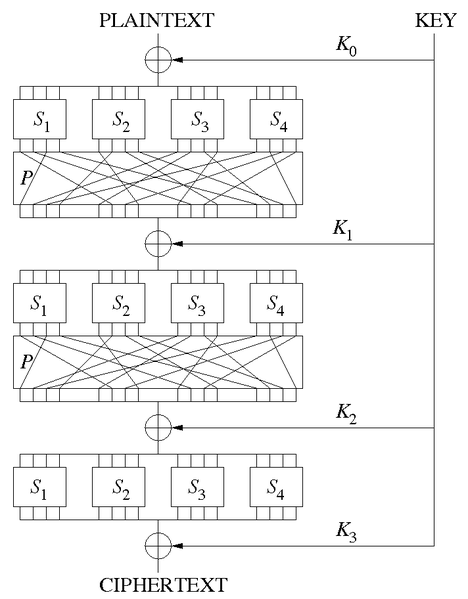
Each round looks like this:
- Combination of the plaintext with the round key (represented by \(\oplus\))
- Substitution of small blocks of bits (referred to as a S-box, or a substitution box)
- Permutation of all the bits (referred to as a P-box, or a permutation box)
The combination of the plaintext with the round key is often XOR, as XOR is easily invertible (\(A \oplus (A \oplus B) = B\), as \(A \oplus A = 0\) and XORing anything against 0 does not change the result.) Decryption, hence, is merely XORing against the corresponding round key. At the same time, the S-box and P-box should also be invertible. This means that decryption for a SPN is merely the reverse process.
A good S-box should offer various properties. Firstly, for it to be invertible, the substitution should be one-to-one. This means that the length of the output should be the same as the length of the input. This allows for decryption. Secondly, changing a single input bit should change about half of the output bits. This is known as the avalanche effect.
A good P-box should ensure that the output bits of any S-box is distributed across the permutation. The reason for doing this is covered in the next section.
By itself, the S-box is a substitution cipher, and the P-box is a transposition cipher. Both ciphers hardly offer any cryptographic strength, as they reveal statistical properties. However, when combined together, they provide powerful cryptographic strength.
Confusion and Diffusion
Confusion and diffusion are key properties of a secure cipher (as identified by Claude Shannon, considered the father of information theory). Confusion refers to the property that each character of the ciphertext depends on several parts of the key, and diffusion refers to the property that when we change a character of the plaintext, then several characters of the ciphertext should change.
Firstly, if a single bit is changed in the plaintext, an S-Box changes several bits. The P-Box then distributes these changed bits across. With several rounds, the ciphertext has changed completely. This satisfies the property of diffusion. Other than having a completely different ciphertext, this also prevents an attacker from modifying the ciphertext in order to get a desired plaintext, as this would change the plaintext drastically.
Secondly, the SPN also exhibits confusion (under the assumption that changing one bit of the key changes several round keys – the SPN does not include derivation of the round keys). Every change in a round key causes a change in the input of the S-Boxes. As per the property of diffusion, the ciphertext would be drastically altered. This means that each of the output bits would depend on several parts of the round keys, which in turn depend on the key. This satisfies the property of confusion.
The power of the SPN lies in how it allows for both properties to be exhibited, despite being so simple and efficient.
Key Schedule
Each round has a certain key of its own, derived from the key given. The algorithm to obtain the round keys is called the key schedule.
With a larger key size, AES has a larger number of rounds. The reason is that given more key bits, there is a need for more rounds so as to ensure that there is confusion. This is why the key schedule differs depending on the key size.
The key schedule derives the first round key from the master key, the second from the first, and so on until all round keys required have been generated. I will not elaborate much on how the key schedule works. The main point to note is that the key schedule consists of shifting bytes and XOR operations. The key schedule is invertible, allowing an adversary to derive the master key given any round key.
A question you may ask is, why not use a cryptographically secure pseudorandom number generator? One could seed the generator with the key, providing a sequence of output round keys that are hard to predict and increasing the difficulty of obtaining the master key from the key schedule.
Simply put, a simpler key schedule provides efficiency but comes at the cost of a bit of security. However, practically speaking, there is not much need to make the key schedule non-invertible.
Despite the weakness of the key schedule, it satisfies the property that changing one bit of the key changes several round keys, which was a requirement for a SPN to be secure.
For more details, you can read Thomas Pornin’s answer on Crypto StackExchange on why a simpler key schedule is used, and poncho’s answer on why making the key schedule non-invertible will not add much security.
SubBytes
A fixed S-box is used, taking in a byte as input and also producing a byte.The S-box of AES is calculated from the multiplicative inverse over \(GF(2^8)\). The presence of multiplicative inverse for all elements is one of the properties that fields satisfy.
A multiplicative inverse for a number \(x\) is a number which when multiplied by \(x\) gives the multiplicative identity \(1\). The multiplicative identity \(1\) satisfies the property that \(x \times 1 = x\). In the field of rational numbers, we call the multiplicative inverse the reciprocal, or \(\frac{1}{x}\).
In a Galois field, there is a more complex procedure used in order to find the multiplicative inverse, known as the Extended Euclidean Algorithm. It turns out that the multiplicative inverses have good non-linearity properties, adding security against attacks which recover the key by exploiting linearity in the S-box.
In addition to the multiplicative inverses, an affine transformation is used which I will not elaborate on. This allows it to be resistant to linear and differential cryptanalysis, as well as algebraic attacks.
For more details on the design of the S-box, look at Rijndael S-box.
ShiftRows and MixColumns
These two operations are what permutates the bits (techincally speaking,
MixColumns does more than just permutations).
ShiftRows just rotates each row by varying number of bytes. The first row is
not rotated, the second row is rotated to the left by one byte, the third row is
rotated to the left by two bytes, etc. This permutates the order of the outputs
from the S-box row-wise.
MixColumns performs a transformation on each column of the matrix. It
multiplies the matrix of bytes with:
\[ \begin{bmatrix} 2 & 3 & 1 & 1 \\ 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 3 \\ 3 & 1 & 1 & 2 \\ \end{bmatrix} \]
in \(GF(2^8)\). Matrix multiplication is composed of several multiplication and
addition operations. This transforms the bytes of every column. Hence,
MixColumns permutates the bits column-wise.
This matrix is a Maximum Distance Seperable matrix. The power of MDS matrices lie in the fact that they have perfect diffusion. Changing \(k\) of the input bytes would change at least \(m-k+1\) of the output bytes, where \(m \times n\) is the size of the matrix.
Combining both operations together, you get a very powerful P-box. As part of a SPN, this P-box helps to ensure diffusion, and does it very well. It propagates changes in the plaintext throughout, making differential cryptanalysis tough.
AddRoundKey
This is just a XOR operation as described in the section on SPNs.
Conclusions on AES
AES remains a very strong cipher. Bruce Schneier, a developer of Twofish, has written in 2000:
I believe that within the next five years someone will discover an academic attack against Rijndael. I do not believe that anyone will ever discover an attack that will allow someone to read Rijndael traffic. So while I have serious academic reservations about Rijndael, I do not have any engineering reservations about Rijndael.
Since then, academic attacks against AES have been developed. But many of them involve a smaller number of rounds or are impractical. The best key-recovery attacks on full AES so far is a biclique attack which is merely faster than brute force by at most a factor of 4. Furthermore, the data storage required works out to trillions of terabytes, far beyond the data stored on the planet.
In addition to its strength, AES performs very quickly. SubBytes and
multiplication in MixColumns can be replaced with a lookup table of 256 bytes.
Its simplicity means that operations can be performed very fast, and is easily
implemented on hardware. All of these properties are why Rijndael was chosen by
NIST to become AES.
If you want to know more about AES, take a look at A Stick Figure Guide to AES. Alternatively, if you want to read more on the design of AES, there’s a comprehensive reference written by the creators themselves, titled The Design of Rijndael.